前回(音楽理論#1)は「メイジャーコードとマイナーコードの違い」についてご紹介しました。
「メイジャーってなに?」「マイナーってなに」「コードがわからない」という方は、過去の記事を合わせてご確認ください!
さて、本題です。
「ドとミは長3度である」この意味がわかりますか?
わかる方はOK!
わからない方は、先へお進みください。本記事を読めば、意味がわかるようになります!
度数とは
度数とは、音程の単位のことを指します。
音程は、音と音との間隔・距離のことでしたね。第1回の時に、以下のように解説していました。
- メジャーコードは、キョリが5つの音程と、キョリが4つの音程の組み合わせでできている
- マイナーコードは、キョリが4つの音程と、キョリが5つの音程の組み合わせでできている
同時に、各音程には名前がついているとも説明していましたが、その名前が度数にあたります。
度数の一覧表
度数の一覧表を作ったので、ご覧ください!
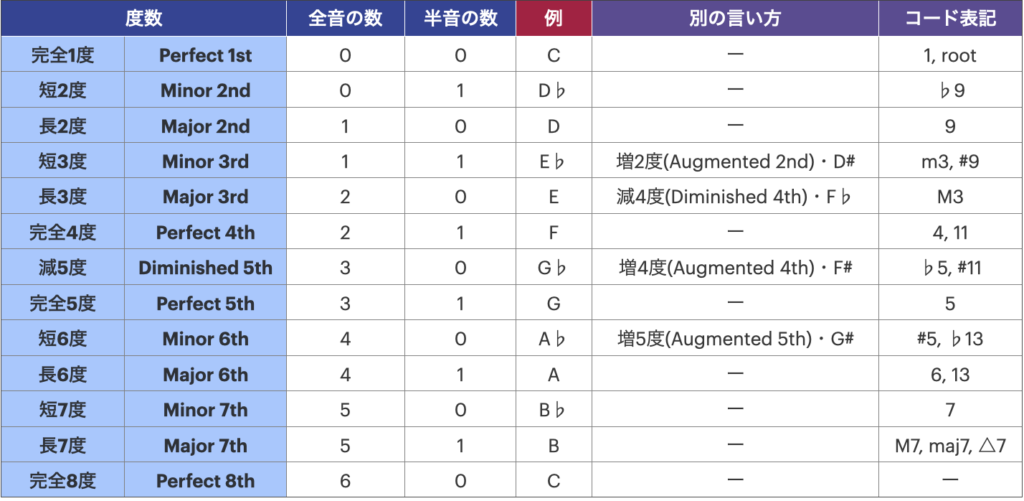

めっちゃあるやん……
って思った方。そうです、めちゃくちゃあります!
しかし、これらも規則性があるため、その規則を掴むことができれば、丸暗記する必要はなくなります。
それでは、表に書かれている内容を1つ1つ解説していきますね。
全音と半音
まず、3列目「全音の数」と4列目「半音の数」についてです。
ひとつ飛ばしの音のことを全音、となりあった音のことを半音と言います。
ピアノの鍵盤で見ると分かりやすいので見ていきましょう。
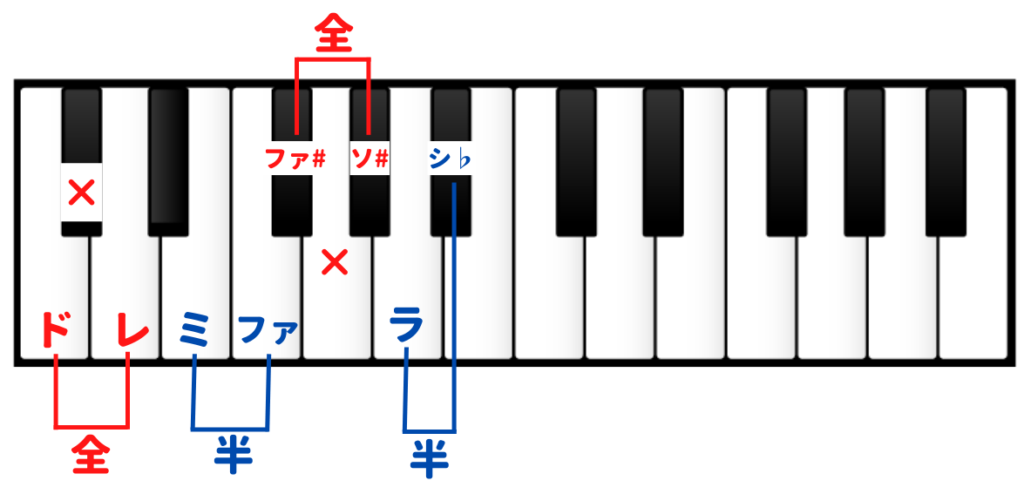
- ドとレは、間にひとつ黒鍵を挟みひとつ飛ばしであるため、全音
- ミとファは、となりあっているため、半音
- ファ#とソ#は、間にひとつ白鍵を挟みひとつ飛ばしであるため、全音
- ラとシ♭は、となりあっているため、半音
全音と半音についてはこんなかんじ。そして、度数というのは、この全音と半音をそれぞれ何個含んでいるかによって名前が決まっているんです!
度数の代表例
それでは、本題の度数についてです。いくつか例を取り上げて説明していきます。
完全1度

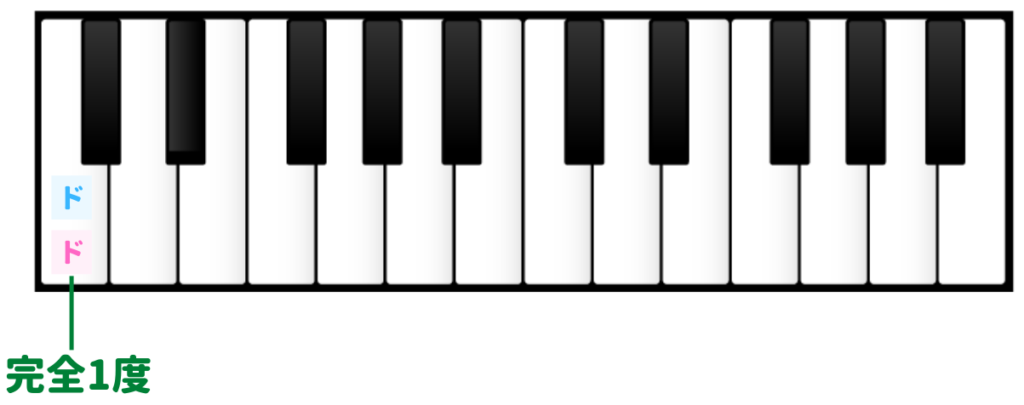
完全1度(Perfect 1st)は、全音の数、半音の数、ともに0。つまり、まったく同じ音という意味です。同じ音であるため、音と音との間に距離はないのですが、これも音程の1種として考えます。

完全って何? 1度の1って何?
という疑問が生じるかもしれませんが、詳しく後で解説していきますので、今はとりあえず「そう言うんだ〜」くらいで考えておいてください!
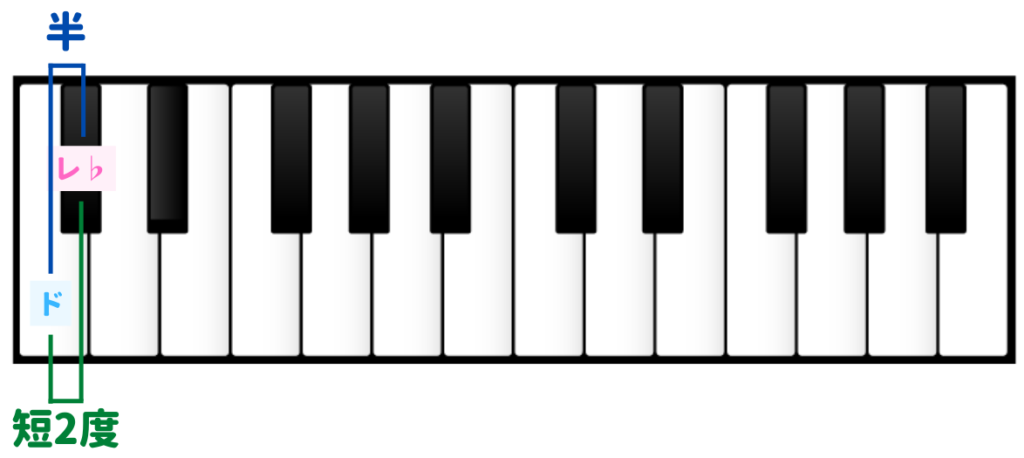
短2度(半音)

短2度(Minor 2nd)は、半音の数が1つ。つまり、半音です。「え、じゃあ半音でいいじゃん」と思われるのはごもっともですが、他の度数の呼び方に合わせて、半音のことを短2度と呼びます。
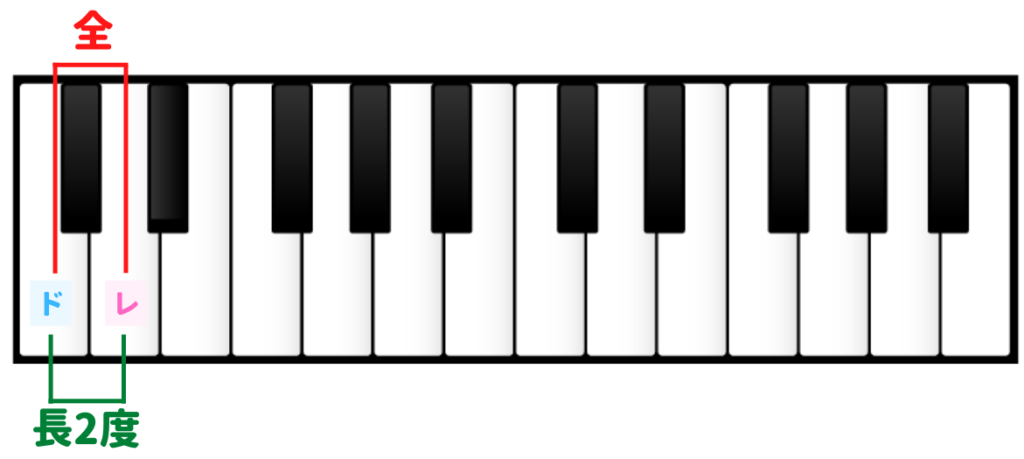
長2度(全音)

長2度(Major 2nd)は、全音の数が1つ。つまり、全音です。短2度のパターンと同じですね。
だいぶ掴めてきたでしょうか。もう少し、例を挙げていきましょう。
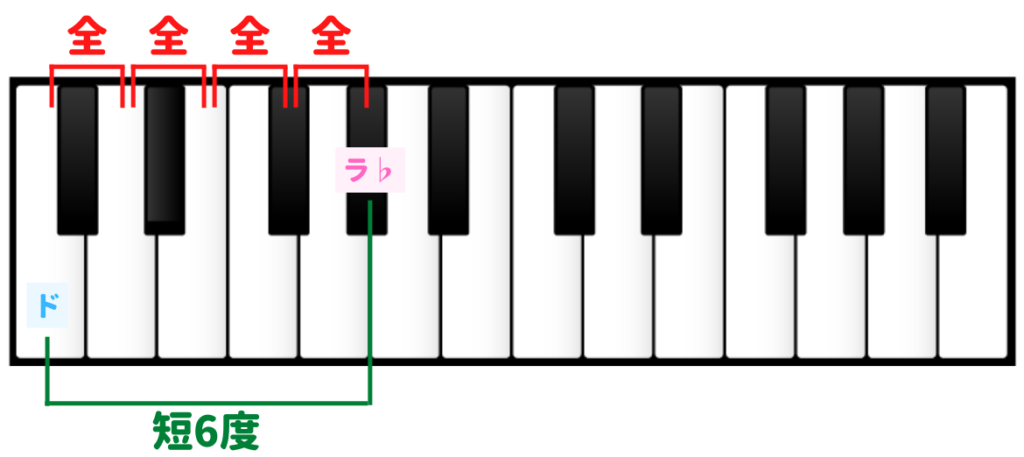
短6度

グッと飛ばしまして、短6度(Minor 6th)。こちらは、全音を4つ組み合わせた音程になります。
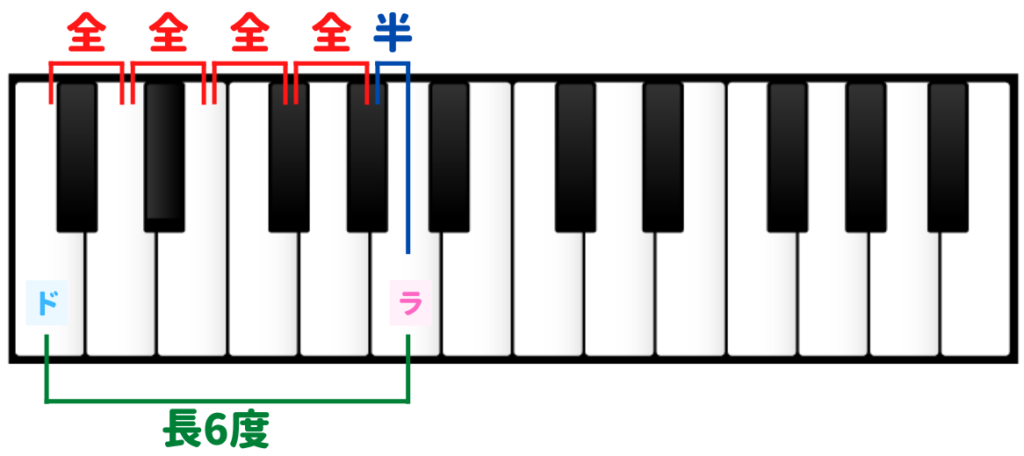
長6度

長6度(Major 6th)は、全音4つと半音1つの組み合わせです。
ここまできたら大丈夫でしょうか。最後、もう1つだけご紹介して、この章は終わります。
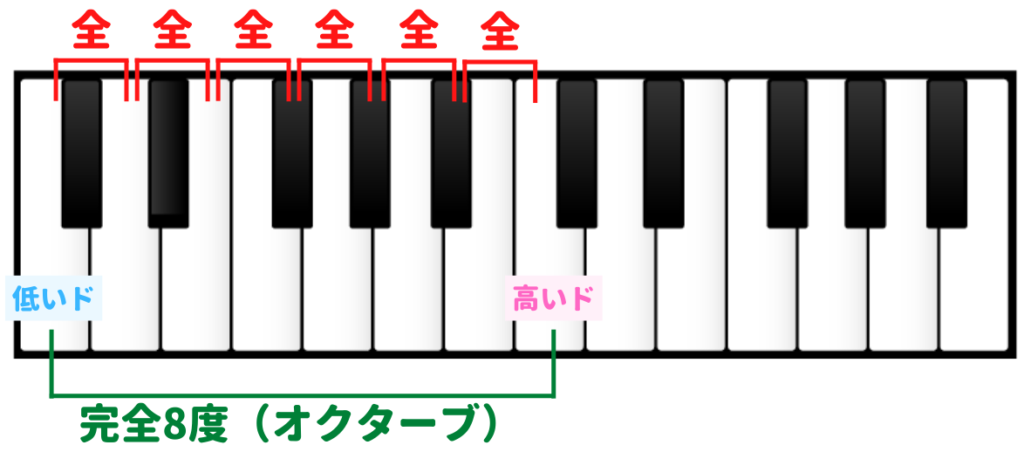
完全8度(オクターブ)

完全8度(Perfect 8th)は、全音の数が6つです。こちらの関係は、オクターブとも呼ばれます。
人は感覚的に、ある音の2±n倍(n:整数)の周波数の音を、元の音と同種の音として捉えます。うん、nとかやめてほしいですね。

例えば、440ヘルツのラの1オクターブ上のラの周波数は、21倍の880ヘルツになるよ
そのため、低いドと高いドは実際には異なる周波数の音であるにも関わらず、同じ音名(=ドレミ)で呼ばれているんですね。現代の音楽で主に使われている十二平均律という音律は、このオクターブを12等分した音律のことを指します。
音律とは、音楽に用いる音高の相対的な関係を決めたもの。
度数に使われている数字
度数に使われている数字は、下の音から何個離れた音名かで決まります。こちらの数字には、シャープやフラットといった考えは出てきません。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ド | レ | ミ | ファ | ソ | ラ | シ | ド |

ドとソの度数は?

ドレミファソ……だから、5度!
長短や完全という文字はとりあえず置いておいて、数字だけであれば指を折り、数を数えることで導き出せます。
下の音がドではない場合も同じです。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ソ | ラ | シ | ド | レ | ミ | ファ | ソ |

ソとミの度数は?

ソラシドレミ……だから、6度!
度数に使われている文字
数字についてわかったところで、度数をややこしくしている文字。長・短・完全・増・減・重増・重減について解説していきましょう。もう少しです! 頑張りましょう!!
度数は、完全系と長短系の2種類に分類されます。
完全系
以下の数字をもつ度数は、完全系に分類されます。
- 1度
- 4度
- 5度
- 8度
なぜ、完全なのか。なぜ、この4つなのか、という問いの答えについては、昔使われていたピタゴラス音律というものが関係しています。数学の授業とかで聞いたことがあるであろう、あのピタゴラスさんです!

呼んだ?
ピタゴラス音律
ピタゴラスは、ある時、弦の長さと振動数が反比例の関係にあることに気がつきます。あ、逃げないで……。音楽と数学や物理は切っても切れない関係なんです。
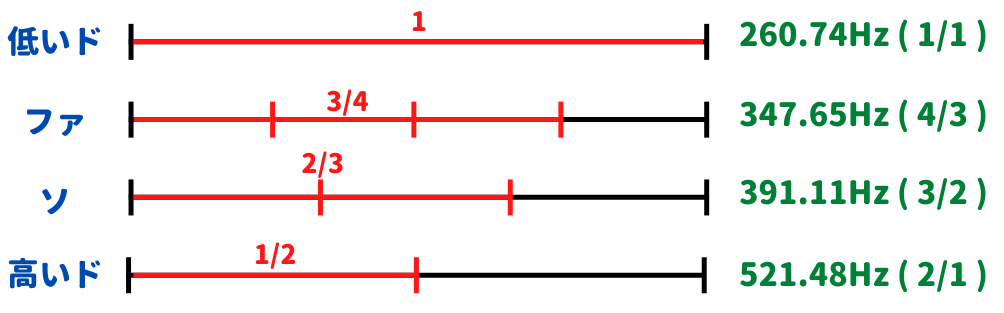
赤い線の部分が、弦が振動するところです。手元にギターやベースがある方は、ぜひ確かめてみてください。開放弦の音からみて完全8度の音が出る12フレットは、弦の長さのちょうど半分(1/2)が振動する仕組みになっています。同様に、完全5度の音が出る7フレットは2/3が振動し、完全4度の音が出る5フレットは3/4が振動しています。
このように、弦の長さが簡単な整数比である場合、美しく調和します!

美しい!!
ピタゴラス音律とは、この美しく調和する度数のうち、基準の音から完全5度上の音、さらに完全5度上の音、または、基準の音から完全5度の下の音、さらに完全5度下の音……を繰り返していくことですべてのドレミを定めた音律のことです。
ピタゴラス音律では、完全1度、4度、5度、8度は協和音となり心地よく響きますが、3度などは不協和音となってしまいます。

しょうがないねえ……

この不協和を解消するために、
ピタゴラス音律を応用した
純正律というものもうまれてるよ
不協和を持つという点に加え、移調や転調ができないという不便さから、ピタゴラス音律や純正律は廃れ、現代では十二平均律が使用されるようになりました。
十二平均律では、実は、うねりが生じない純正音程は完全1度と完全8度しかありません。しかし、ピタゴラス音律や純正律時代の名残で、4度や5度も、完全4度、完全5度と呼ぶ習慣になっています。
完全系における増・減の考え方
ドとソは、完全5度です。では、ドとソ♭の度数は何になるでしょうか。
数字は、ドレミファソですので、5で間違いありません。しかし、ソとソ♭は異なる音。どこかで区別を付けなければいけません。そこで、完全という文字を減に置き換えます。つまり、ドとソ♭の度数は、減5度になります。
では、ソから半音上がったソ#はどうなるでしょうか。減の反対の増に置き換えて増5度になります。
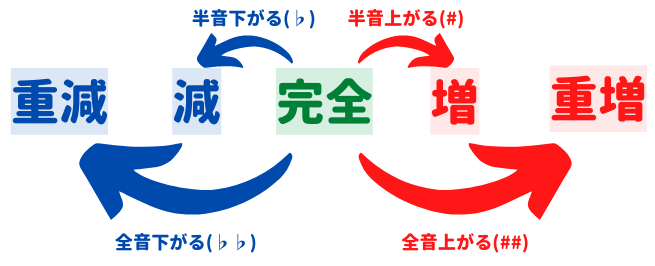
ダブルシャープ(##)やダブルフラット(♭♭)は、それぞれ重増・重減という文字に置き換えられます。
長短系
長短系は完全系以外と覚えるのが早いです。
以下の数字をもつ度数は、長短系に分類されます。
- 2度
- 3度
- 6度
- 7度
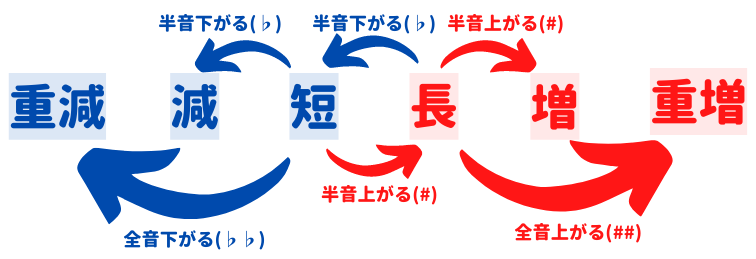
増減の考え方は、ほとんど完全系と同じですが、長から半音下がったら短、短から半音上がったら長という、長短系特有のルールもあります。
まとめ
最後まで、ご覧いただきありがとうございます!
度数について、理解が深まったでしょうか?
度数の組み合わせによって、「コード(和音)」や「スケール(音階)」ができあがります。
もちろん、度数を知らなくても演奏はできますし、「音楽理論の知識」=「楽器や歌のうまさ」ではありません。
しかしながら、「もっと音楽を深く理解したい」場合は、避けて通れないものです。
ここまで読んでくださった皆さまは、1歩リードです!
他にも音楽理論の記事がございます。よろしければ、あわせてご覧ください!
また、YouTubeでも、音楽理論の解説などをおこなっています。
フリーアトリエ晴星(YouTubeチャンネル)
いちど、ご視聴いただけると嬉しいです☺️